2D Bond-Orientational Order for Lipid Membranes

I discuss the use of 2D Bond-Orientational Order to describe lipid phase in membrane and the use of projections to address membrane undulation when measuring.

The 2D Bond-Orientational Order Parameter

This past year, the famous 2D Bond-Orientational Order parameter, originally developd by Nelson and Halperin,[1] recieved some of the spotlight as part of the Nobel Prize in Physics, awarded to Thouless, Haldane, and Kosterlitz ”for theoretical discoveries of topological phase transitions and topological phases of matter.” It has been used to describe solid, “hexatic”, and liquid phases of 2D systems. To describe bond-orientations of n-fold order around the kth particle in a system with n nearest neighbors, each indexed as l, the order parameter is:

\[\Psi_n^k = \frac{1}{n}\sum^n_{l\ \epsilon\ nn(k)} \exp[in\theta_{lk}] = \frac{1}{n}\sum^n_{l\ \epsilon\ nn(k)} \cos(n\theta_{lk}) + i\sin(n\theta_{lk})\]

But typically only \(\Psi_6^k\) is used as an order parameter:

\[\Psi_6^k = \frac{1}{n}\sum^n_{l\ \epsilon\ nn(k)} \exp[i6\theta_{lk}]\]

where the angle \(\theta_{lk}\) is evaluated using an arbitrary, constant reference vector. By doing this measurement, we get a complex vector which tells us the orientation of the hexagon and when we take norm of this complex vector (|\(\Psi_6^k\)|) we get a number between 0 and 1 which tells us how close to a hexagon the orientation of l points around k are.

Often when I’ve explained this order parameter to a colleague in chemistry it has been difficult to help them understand. Please see the following illustration, which should help your understanding of \(\Psi_6^k\):

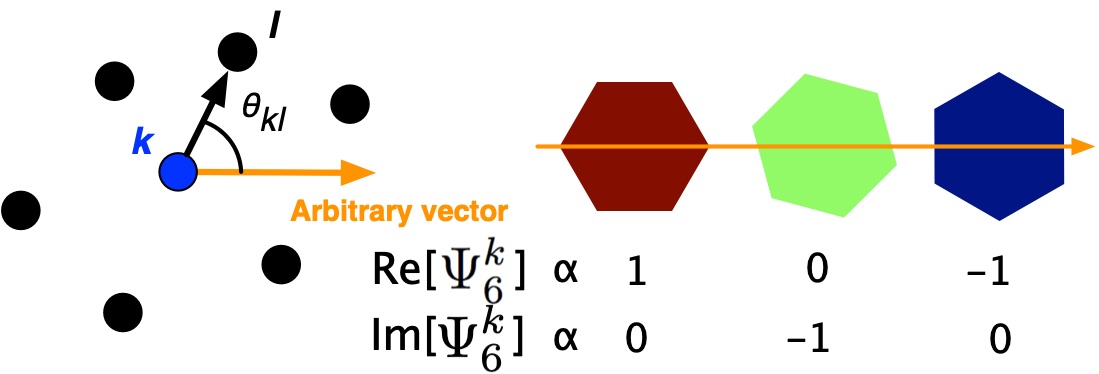
Figure: (Left) Illustration of a particle k and it’s six nearest neighbors, indexed by l, along with the reference vector, which is often selected to be (x,y) = (1,0). (Right) The orientation of the conceptual hexagon defined by nearest neighbors of k, which can be described by the real (or imaginary) parts of \(\Psi_6^k\).

\(\Psi_6^k\) and positional pair correlation functions are used to describe phases in 2D

For many years the character of 2D phase transitions in hard disks (2D circles that cannot overlap each-other but have no attractive or repulsive forces) has been debated. A 2011 paper by Barnard and Krauth, along with some follow-up papers, seem to have put the debate to rest.[2]

Pair-wise distance (r) correlation functions of \(\Psi_6^k\) (g₆(r)) and position (g_G(r)) have been used to identify solid, hexatic, and liquid 2D phases. This is done based on the functional form of decay of the correlation over pair-wise distance in the Kosterlitz-Thouless-Halperin-Nelson-Young (KTHNY) theory of 2D melting:

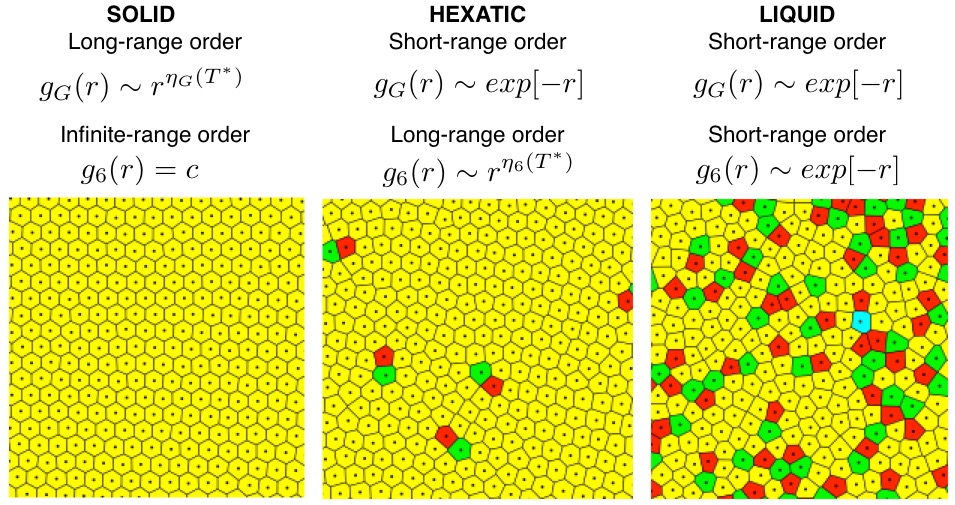
Figure Example Voronoi tessellations of 2D systems in the solid, hexatic, and liquid state. Pair correlation functions of position (g_G(r)) and \(\Psi_6^k\) (g₆(r)). \(T^* = k_{\text{B}}T/<U>\). Voronoi tessellations credited to N. Vandewalle at GRASP.[3]

Interest in lipid bilayers

We may use this order parameter as a method to distinguish the thermodynamic phase of lipids. In the case of lipid phase separations to liquid ordered (L_o) and disordered (L_d) domains, we are able to see that the packing of each lipid (|\(\Psi_6^k\)|) is clearly different between phases, though the bond-orientations of lipids (\(\Psi_6^k\)) are uncorrelated, as expected of any liquid state.

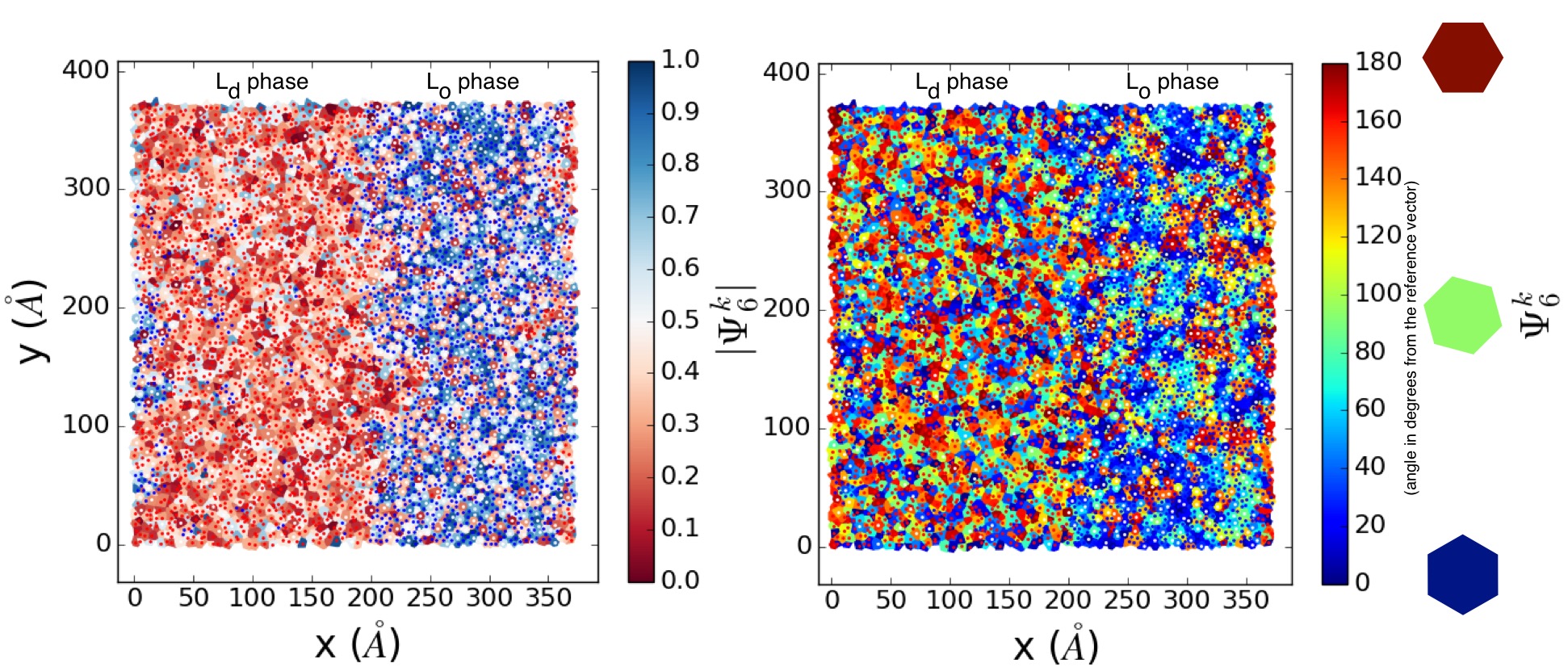
Figure Tessellations of a phase separated 5406-lipid bilayer. Blue, red, and white dots represent lipid tails belonging to DPPC, DIPC, and CHOL lipids in the membrane. (Left) |\(\Psi_6^k\)| shows clear separation between the packing lipid domains, though \(\Psi_6^k\) shows the bond-orientation of lipids is not substantially different between L_o and L_d phases.

We should also consider the following: Lipid bilayers are not simply 2D. There are undulations to the membrane surface that would, if not addressed, distort the measurement of \(\Psi_6^k\), as angles from the reference vector would include height mismatchings of the measured atoms. I address this via a plane fitting approach.

Plane-fitted measurement of \(\Psi_6^k\)

To address height mismatches of a lipid tail’s nearest neighbors, I fit a lipid tail and its six nearest neighbors to a plane of best fit, project the coordinates and reference vector into the plane, and measure \(\Psi_6^k\) there.

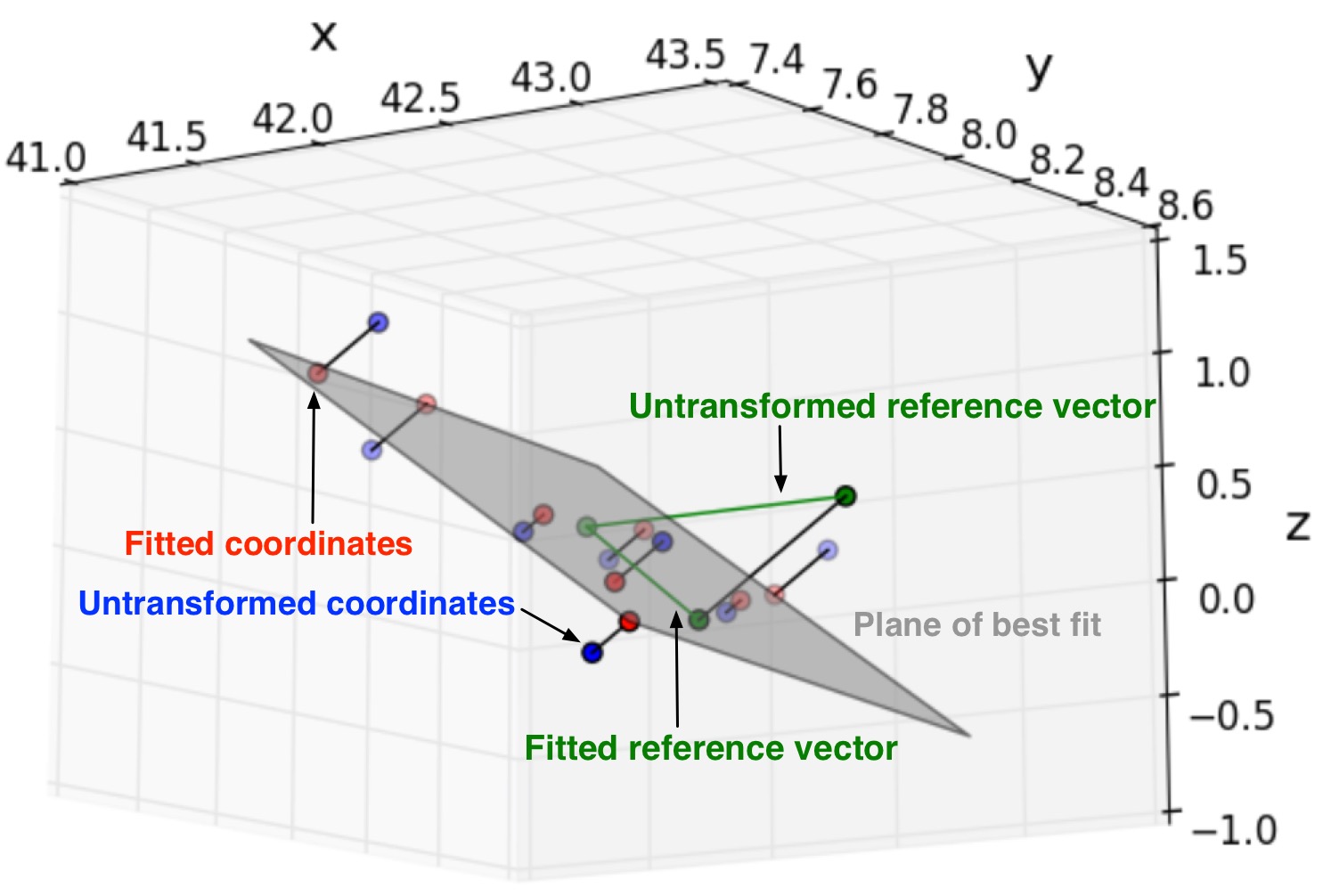
Figure: Coordinate representing a MARTINI lipid tail with coordinates representing its six nearest neighhbor tails transformed to lie on a plane that best-fits all seven points. The reference vector is transformed to lie in the plane as well. In this particular application, C2A, C2B (D2A, D2B) beads of DPPC (DIPC) are selected and the centroid of R[1-5] of CHOL are selected to represent lipid tails.

If you’d like to check out an example script written to analyze MARTINI DPPC, DIPC, and CHOL lipid membranes using the MDAnalysis library to find these coordinates, please check out my github. Additionally, a sample of trajectory data from our 2018 work examining the effects of MARTINI cholesterol from low to high concentrations is available, along with scripts that can produce Voronoi tessels colored by \(\Psi_6^k\) and \(\|\Psi_6^k\|\) are available.

An additional interesting application of \(\Psi_6^k\) was around the same time as we applied \(\Psi_6^k\) for examining ternary lipid mixtures for elucidating a “hexatic-like” lipid phase of DPPC with the MARTINI coarse-grained model.[4]

Please cite:
G.A. Pantelopulos, T. Nagai, A. Bandara, A. Panahi, & J.E. Straub “Critical size dependence of domain formation observed in coarse-grained simulations of bilayers composed of ternary lipid mixtures,” J. Chem. Phys. 147, 095101 (2017) G.A. Pantelopulos & J.E. Straub “Regimes of Complex Lipid Bilayer Phases Induced by Cholesterol Concentration in MD Simulation,” Biophys. J. 115, 2167–2178 (2018)

References:

1. B.I. Halperin & D.R. Nelson “Theory of Two-Dimensional melting,” Phys. Rev. Lett. 41, 121–124 (1978).
2. E.P. Bernard & W. Krauth “Two-Step Melting in Two Dimensions: First-Order Liquid-Hexatic Transition,” Phys. Rev. Lett. 107, 155704 (2011).
3. J. Schockmel, E. Mersch, N. Vandewalle, & G. Lumay, “Melting of a confined monolayer of magnetized beads,” Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys. 87, 1–7 (2013).
4. S. Katira, K.K. Mandadapu, S. Vaikuntanathan, B. Smit, & D. Chandler “Pre-transition effects mediate forces of assembly between transmembrane proteins,” Elife 5, 1–8 (2016).