How to Determine When a Lipid Bilayer is Phase Separated

I discuss the definition of lipid miscibility point used in experiment and determine the equivalent size-depedndent binary mixing entropy for a 2D lattice.

How do we know when a lipid bilayer is phase separated?

Several people working on simulations of lipid phase separation have asked the question “How do I know when a bilayer is really phase separated?” There is no obvious answer. The degree of any anisotropic mixing within any system seems to behave as a continous transition as dependent on various variables, such as temperature, system size, or relative concentration of types of molecules.

What would be very convenient for people performing simulations of phase-separating systems, though, is to find a way to relate their results to experimental observations.

In the case of lipid bilayers, experimentalists have defined the “miscibility point,” at which they assign miscibiliy temperatures, to correspond to the point where 50% of liquid ordered (L_o) domain-forming lipids are miscible with liquid disordered (L_d) domain-forming lipids. For example, in the works of Bakht and London, they prepare small unilamellar vesicles (SUVs) of phase-separating lipid mixtures and measure the flourescence of probes (of fluorescence F) which are quenced in the presence of L_d phase (of fluorescence F₀), and report the ratio F/F₀.[1,2] As a function of temperature, the ratio F/F₀ follows a sigmoid function as dependent on temperature, and the inflection point of this function is believed to correspond to 50% miscibility of L_o and L_d domains, where they assign the miscibility teperature.

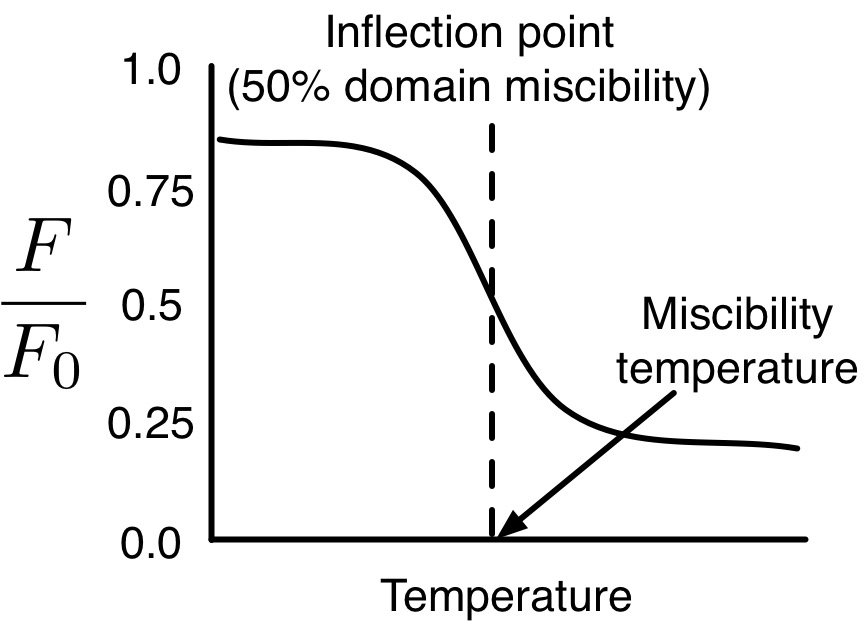
Figure: Illustration of F/F₀ fluorescence measurement used to determing miscibility point, which is assigned as the point of inflection in F/F₀(T).

Veatch and Keller also assign the “miscibility point” to corespond to the point when 50% of L_o domain-forming lipids are miscible with L_d domain-forming lipids in giant unilamellar vesicle (GUV) fluorescence experiments.[3,4] We can find the point where 50% of L_o domain-forming lipids are miscible with L_d domain-forming lipids simulation by evaluating the mixing entropy of a binary mixture on a hexagonal lattice monolayer, which happens to be very similar to a lipid bilayer for a few reasons.

% Miscibilities of binary mixtures on 2D hexagonal lattices

Each monolayer of a lipid bilayer can easily be thought of as a quasi-2D structure, and just like any 2D surface, lipids within monolayers are, on average, coordinated with six surrounding lipids.[5] Additionally, phase-separated bilayers (paticularly macroscopic separations, visible via microscopy) show strongly regstered domains – that is, L_o domains lie on top of L_o domains, and L_d domains lie on top of L_d domains.[6] Because of this, thinking about phase-separated lipid bilayers as finite-sized periodic 2D hexagonal lattices seems quite reasonable, as this should be similar to the conditions of a lipid bilayer simulation.

In a previous post I discussed the measurement of lipid mixing entropy using voronoi tessellations of lipid leaflets. The very same definition of mixing entropy will be used here for the binary case (E=2),

\[S_{mix} = -p_1 \log_2(p_1) -p_2 \log_2(p_2),\]

in which \(p_1\) corresponds to the fraction of contacts between lipids of the same type and \(p_2\) to the fraction betweens lipids of a different type.

A phase separation is necessarily defined by an interface. In this case, we consider the phase separation to manifest a linear interface, partitioning the system to left and right sides, as occurs in MD simulations of lipid phase separation. Assuming there are N lipids in the monolayer, and the x- and y-dimensions of the system are equal (as they are in the vast majority of lipid membrane simulation literature), each interface will be composed of \(\sqrt{N}\) lipids, such that the interfaces contain \(2\sqrt{N}\) lipids in total.

In a phase separation in which the two domains are truly pure, the only contribution to mixing entropy will come from the interface, and because the interface is dependent on the number of lipids, N, the mixing entropy of a phase separation is dependent on N. As such, it happens that \(p_1 = (N - 2\sqrt{N} + 2\frac{2}{3}\sqrt{N})/N\) and \(p_2 = (2\frac{1}{3}\sqrt{N})/N\). The following figure illustrates this point:

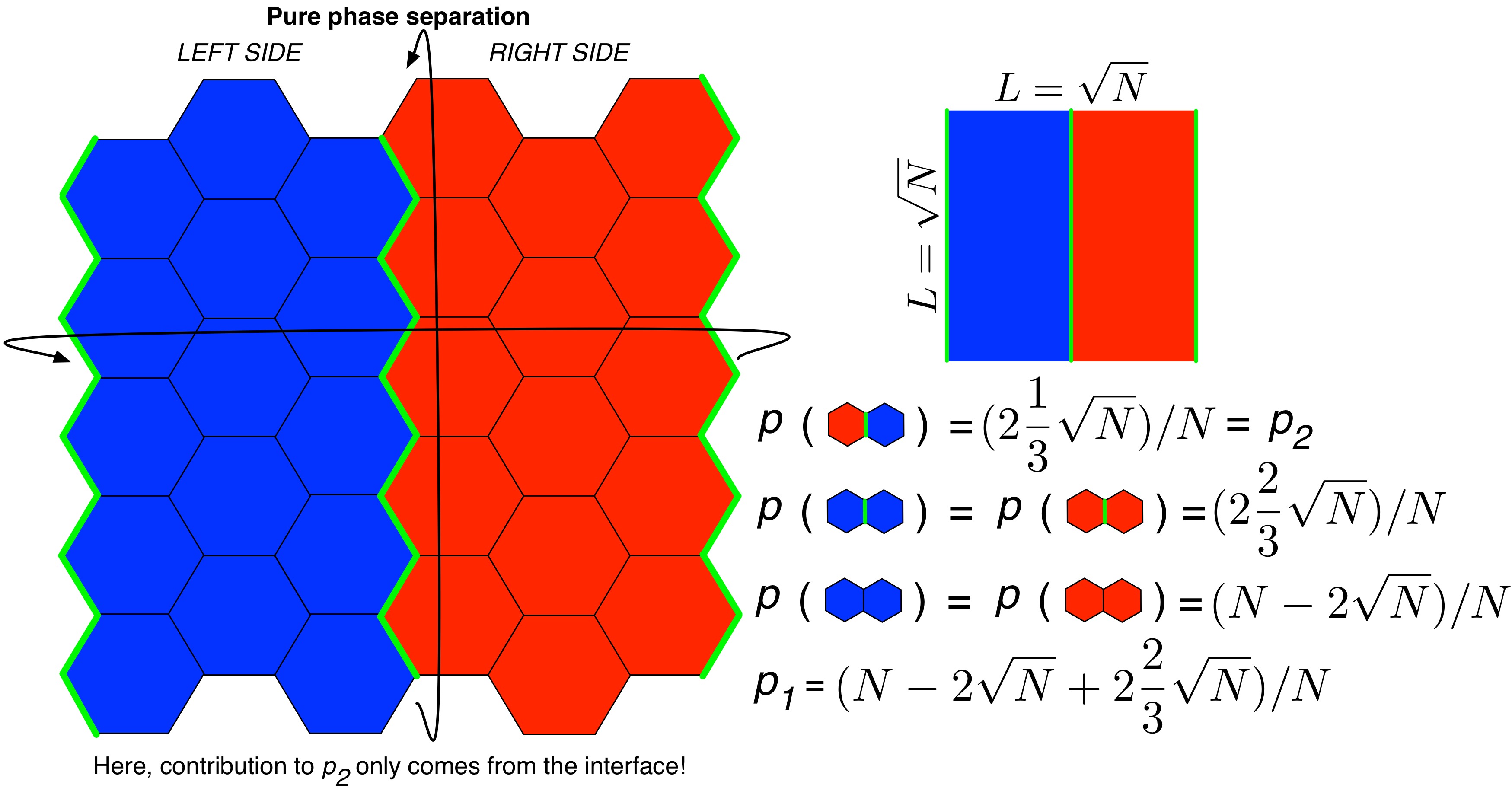
Figure: Illustration of a pure binary phase separation on a hexagonal lattice. The two types of lipids are represented in red and blue, respectively, and the interfaces between domains are drawn with a bold green line.

To determine the mixing entropy of a system at 50% miscibility, or more precisely, where the system should be expected to exhibit 50% of its maximum fluorescence, we add in a background “phase” consisting 50% of all lipids in an ideally-mixed (miscible) state, such that the remaining, pure domains of the system would contribute 50% of the maximum fluorescence signal. This requires the definition of an additional interface between pure and mixed phases, and the contribution of the ideally-mixed domian to the mixing entropy.

While developing the 50% miscibility case, we may as well write equations that describe \(S_\mathrm{mix}\) as dependent on any % miscibility as well. We can introduce another parameter, \(\Phi = \frac{\%\ miscibility}{100\%}\) to represent the miscibility. Lipids involved in the interface between pure and mixed phases contribute \(\frac{7}{10}\sqrt{N}/N\) to \(p_1\) and \(\frac{3}{10}\sqrt{N}/N\) to \(p_2\) while lipids in the ideally mixed phase contribute \(\frac{1}{2}N_\mathrm{D}\Phi/N\) to \(p_1\) and \(p_2\), where \(N_\mathrm{D} = N - 3\sqrt{N}\), the number of lipids with phases that are not at an interface (we lose one pure-pure interface when introducing the ideally mixed phase):

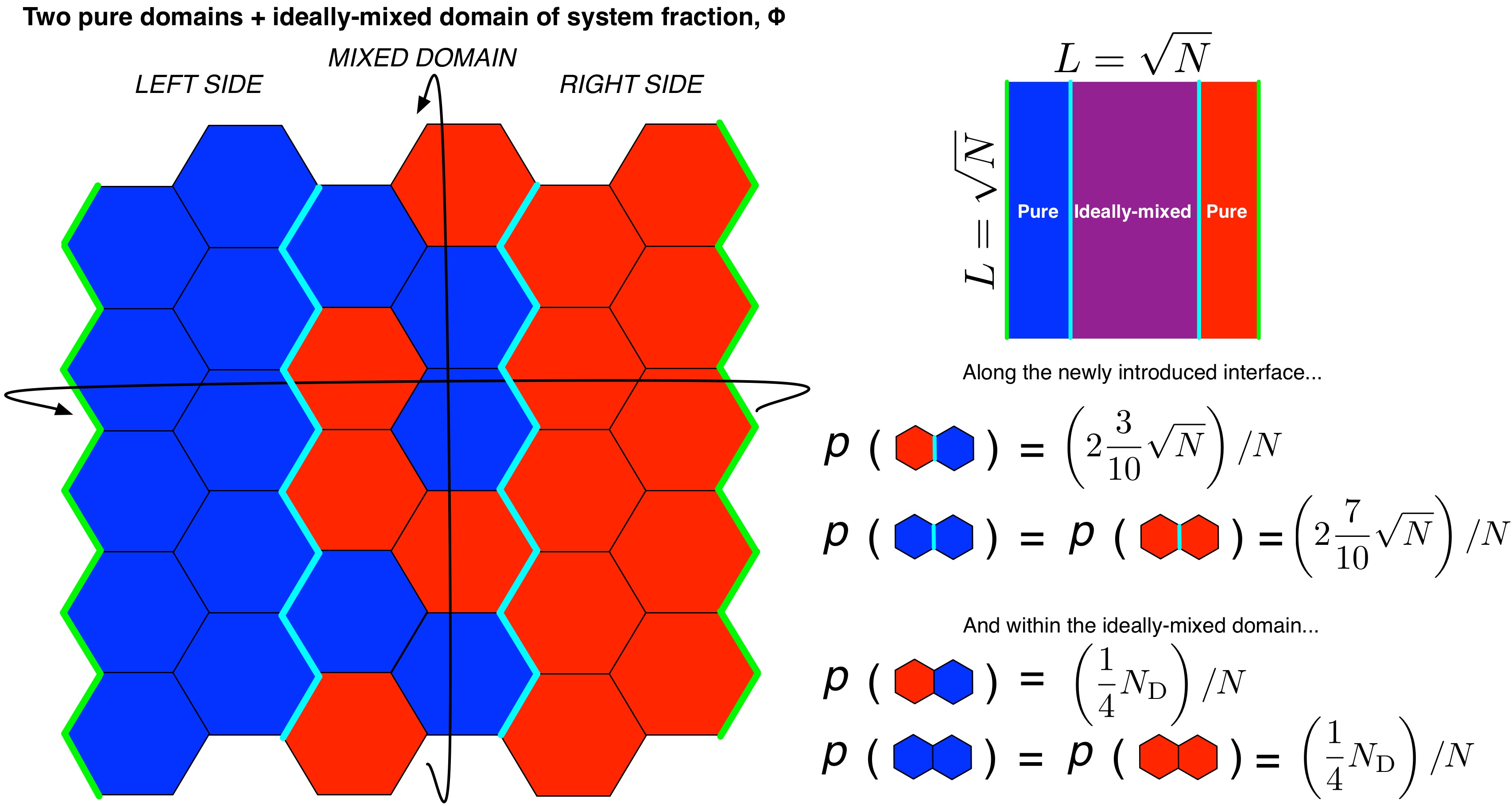
Figure: Illustration of pure domains in a binary mixture coexisting with an ideally-mixed domain composing a fraction (\(\Phi\)) of the system. The two types of lipids are represented in red and blue, respectively, the interfaces between pure domains are drawn with a bold green line, and the interfaces between ideally-mixed and pure domains are drawn with a bold cyan line.

With these additions, we can write

\(p_1 = \left( \left(N_\mathrm{D} - N_\mathrm{D}\Phi \right) + \frac{1}{2}N_\mathrm{D}\Phi + \frac{2}{3}\sqrt{N} + 2 \frac{7}{10}\sqrt{N} \right) / N\), \(p_2 = \left( \frac{1}{2}N_\mathrm{D}\Phi + \frac{1}{3}\sqrt{N} + 2 \frac{3}{10}\sqrt{N} \right) / N\),

which may be used to determine the mixing entropy, \(S_{mix}\) corresponding to some % miscibility, and vice-versa. This allows us to describe the “extent of mixing” of these systems in a way that is easy to conceptualize, and is directly relateable to experiment, from the results of lipid bilayer simulations.

Last, for fun, let’s see how several different amounts of miscible phase change with N:

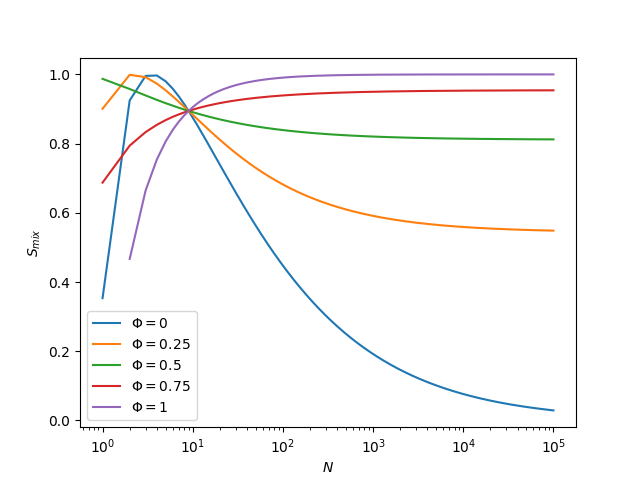
Figure: Binary mixing entropies computed for various amounts of ideally-mixed domain as they depend on \(N\).

We can see that \(\sqrt{10}\) is very special. This is because \(\sqrt{10}\) is the inflection point in the positive domain of the function \(\sqrt{N}\). Small values such as 10 are far, far too small to experience macroscopic phase separation, so this point does not matter very much.

For more details on finite size effects in lipid bilayer phase separation, I urge you to read our recent work in JCP: G.A. Pantelopulos, T. Nagai, A. Bandara, A. Panahi, & J.E. Straub “Critical size dependence of domain formation observed in coarse-grained simulations of bilayers composed of ternary lipid mixtures,” J. Chem. Phys. 147, 095101 (2017)

Also, a special thank you to Tetsuro Nagai for helpful discussion about this post.

References:

1. O. Bakht, P. Pathak, & E. London “Effect of the Structure of Lipids Favoring Disordered Domain Formation on the Stability of Cholesterol-Containing Ordered Domains (Lipid Rafts): Identification of Multiple Raft-Stabilization Mechanisms.,” Biophys. J. 93, 4307–4318 (2007).
2. Megha, O. Bakht, & E. London “Cholesterol precursors stabilize ordinary and ceramide-rich ordered lipid domains (lipid rafts) to different degrees: Implications for the bloch hypothesis and sterol biosynthesis disorders,” J. Biol. Chem. 281, 21903–21913 (2006).
3. S.L. Veatch, & S.L. Keller “Separation of Liquid Phases in Giant Vesicles of Ternary Mixtures of Phospholipids and Cholesterol,” Biophys. J. 85, 3074–3083 (2003).
4. S.L. Veatch, & S.L. Keller “Seeing spots: Complex phase behavior in simple membranes,” Biochim. Biophys. Acta - Mol. Cell Res. 1746, 172–185 (2005).
5. K. Kim, S.Q. Choi, Z.A. Zell, T.M. Squires, & J.A. Zasadzinski “Effect of cholesterol nanodomains on monolayer morphology and dynamics,” Proc. Natl. Acad. Sci. 110, E3054–E3060 (2013).
6. M.C. Blosser, A.R. Honerkamp-Smith, T. Han, M. Haataja, & S.L. Keller “Transbilayer Colocalization of Lipid Domains Explained via Measurement of Strong Coupling Parameters,” Biophys. J. 109, 2317–2327 (2015).