Lipid Mixing Entropy with Voronoi Tessellation

I discuss mixing entropy as an order parameter for lipid mixing and describe a Voronoi tessellation-based method and calculation using MDAnalysis and scipy.

Lateral Heterogeneity in the Cell Membrane

Membranes are composed of an incredibly complicated mixture of proteins, lipids, and glycomolecules. There can be many domains of molecules over the surface of the membrane which are structurally distinct. Protein structures and thus functions can be different depending on what kind of domain they sit within. For many years people have worked to understand how these domains form.

There are over one hundred lipids that may compose a cell membrane. These mix together, increasing the entropy of the mixture until the enthalpic benefit of interacting with similar lipids and the entropic benefit of mixing with different lipids balance out.

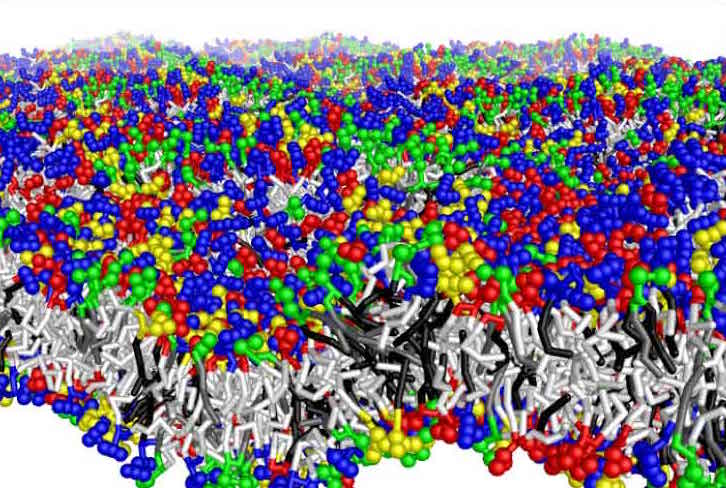
Figure: Complex mixture of a plant membrane constructed with coarse-grained lipids by Marrink and coworkers.

Lipid Mixing Entropy

To quantify how “mixed” a lipid membrane is, many have employed a measure of “mixing entropy” (S_mix). The most common way this has been done is by gridding each leaflet of the membrane in to N regions and counting the fraction of each j^th lipid (p_j) of M lipid types within each i^th region, and then taking the mean of the entropies calculated for all regions[1]:

\[S_{mix} = -\frac{1}{N_{regions}} \sum^{N_{regions}}_{i=1} \sum^{M}_{j=1} p_j(i) \log(p_j(i))\]

However, this method is limited in that the solution is dependent on how the system is split into these regions. Other methods rely on the identification of nearest neighbors requiring selection of cutoffs for neighbor detection or separation of the system into regions.[2] Ideally, the mixing entropy should be measured without any kind of cutoff or gridding scheme that can influence the result.

Voronoi Edge Lipid Mixing Entropy

In a 2017 paper about finite size effects of lipid domain formation we developed and employed a novel method of evaluating mixing entropy using Voronoi tessellations of lipid head groups. This method is quite simple in that it involves counting Voronoi edges formed between pairs of lipids. With this method there is no need to separate the system in to regions or to use arbitrary cutoffs for determining the neighbors of lipids. The mixing entropy is simply written as

\[S_{mix} = -\sum^{E}_{j=1} p_j \log_E(p_j),\]

where there are E types of voronoi edges and we find the probability of the j^th type of voronoi edge. These “types” of voronoi edges are unique types of contacts formed by a pair of lipids sharing a voronoi edge. For example, lipidA-lipidA, lipidB-lipidB, …, lipidZ-lipidZ are all the same kind of voronoi edge – they are edges between the same type of lipid to the same type of lipid. However, lipidA-lipidB, lipidA-lipidC, lipidB-lipidC are all different types of edges. As such, in a two-lipid system E=2, in a three-lipid system E=4, in a four-lipid system E=7, in a five-lipid system E=11 and so on. The log is in the base of E such that the maximum value of S_mix is always 1.

In recently submitted work we used this method to calculate the mixing entropy only considering DPPC and DIPC lipids in a ternary mixture which includes cholesterol. As such, we only evaluated DPPC-DPPC = DIPC-DIPC and DPPC-DIPC Voronoi edges.

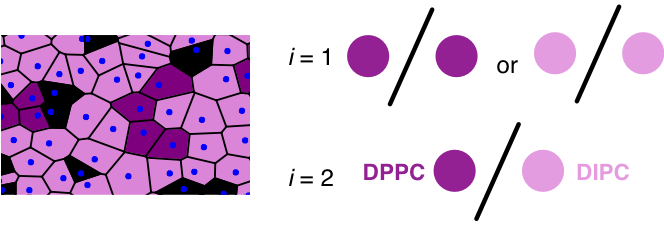
Figure (Left) Visualization of a Voronoi Tessellation of lipid head group (x,y) coordinates (blue) in a slice of a DPPC (purple), DIPC (pink), and cholesterol (black) mixture. (Right) Cartoon showing each type of voronoi edge when evaluating mixing entropy of only DPPC and DIPC.

A python implementation of this method (with contribution from Asanga Bandara) used to tessel DPPC-DIPC-CHOL mixtures in the Martini coarse-grained model using scipy, MDAnalysis to get (x,y) coordinates of lipid head groups, and multiprocessing for parallization with OpenMP is available on my github.

Please cite:
G.A. Pantelopulos, T. Nagai, A. Bandara, A. Panahi, & J.E. Straub “Critical size dependence of domain formation observed in coarse-grained simulations of bilayers composed of ternary lipid mixtures,” J. Chem. Phys. 147, 095101 (2017)

References:

1. M. Camesasca, M. Kaufman, & I. Manas-Zloczower “Quantifying Fluid Mixing with the Shannon Entropy,” Macromol. Theory Simulations 15 595–607 (2006).
2. G.B. Brandani, M. Schor, C.E. MacPhee, H. Grubmuller, U. Zachariae, & D. Marenduzzo “Quantifying Disorder through Conditional Entropy: An Application to Fluid Mixing,” PLoS One 8 e65617 (2013).